1. Введение.
Человек — существо социальное. Объединение отдельных людей в группу изменяет некоторые стороны их психической деятельности, существенно меняя скорость, силу и характер их реакций на внешнюю ситуацию. Свойства группы как целостного психосоциального объекта определяются, с одной стороны, психофизиологическими свойствами отдельных её членов, с другой — структурой межличностных связей в группе.
Поведение человека в определённой обстановке не может быть правильно понято без учёта параметров коллектива, которому он в данной ситуации принадлежит.
Идея конструирования социальной группы, обладающей заданными свойствами, не нова. В настоящей работе мы попытаемся подойти к проблеме формирования группы с позиции структуры интертипных отношений. Разработанный А. Аугустинавичюте типологический подход к межличностным отношениям [1, 3, 4] предоставляет нам такую возможность.
Здесь в качестве объекта исследования будут рассматриваться малые группы, отличающиеся друг от друга спектром интертипных отношений.
2. Теоретический анализ.
Типология различных пар подробно описана в работе А. Аугустинавичюте [1]. В таблице 1 представлена полученная в работе [2] группа признаков дихотомии социона [2]. Не останавливаясь здесь на классификации пар, отметим только, что для любого типа пары, а их всего 15, имеется, как видно из таблицы 1, совпадение элементов по семи признакам и несовпадение по восьми. Можно сказать, что в паре происходит нейтрализация восьми биполярных признаков.
Для идентификации типа требуется четыре ортогональных признака, т. е. пространство типа четырехмерно. Размерность пространства пары на единицу меньше — для идентификации пары нужна тройка ортогональных признаков (табл. 1).
Рассмотрим теперь группы, пространство которых двумерно, а именно, четвёрки, получающиеся при разбиении социона двумя биполярными признаками. Общее количество таких разбиений равно количеству сочетаний из пятнадцати по два:

Однако для троек взаимозависимых признаков, например X13, X14, X15, результаты, разбиения социона парами X13X14, X14X15, X13X15 будут совпадать. Таким образом, количество таких разбиений множества из шестнадцати типов на четыре части по четыре типа будет:

Каждому такому разбиению соответствует тройка признаков:

Таблица 1. Признаки дихотомии социона:
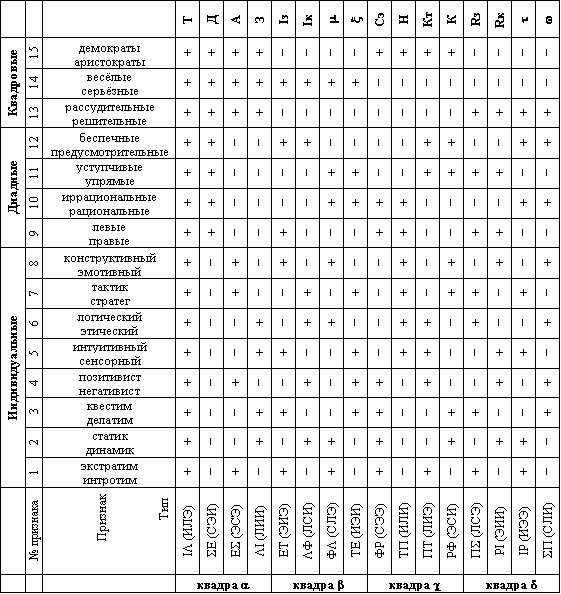
Таблица 2. Таблица умножения для тройки взаимозависимых признаков.

Типичный пример такой группы — квадра, где D диады располагаются на скрещивающихся рёбрах (например, P1).
Аналогичная ситуация будет наблюдаться и для всех остальных тридцати четырёх разбиений. В таблице 3 приведены все тридцать пять возможных разбиений социона на четвёрки парами ортогональных признаков.

Оказалось, что полученный класс малых групп распадается на два существенно отличающихся друг от друга подкласса.
1. Группы, у которых все элементы находятся в одинаковой интертипнойситуации, представленной набором из трёх симметричных отношений. Этот подкласс содержит пятнадцать разбиений. Назовём такие группы однородными, или гомогенными.
2. Разбиения на неоднородные группы. В них тоже три вида отношений. Однако одна пара типов, находящихся в симметричном отношении, — дуализации — пребывает в более выгодной интертипной ситуации по отношению к другой такой паре. Неоднородных групп всего двадцать.
Большинство этих групп абсолютно не изучены и представляют несомненный интерес в плане расширения наших представлений о типах малых групп и их свойствах.
Если символу отношения придать смысл оператора, переводящего один тип в другой, то все шестнадцать отношений в соционе образуют коммутативную группу шестнадцатого порядка. Групповой операцией при этом является переход из типа в тип, а единицей — отношение тождества — тождественный переход. Отношения в четвёрке вместе с тождественным отношением образуют коммутативную группу четвёртого порядка, это объединение типов замкнуто относительно интертипных отношений и обладает свойствами целого. Такая четвёрка, являясь некоторой проекцией социона, действует в нём, как целое в целом, поэтому в дальнейшем будем полученные здесь однородные и неоднородные группы называть целостными.
Приложение.
Анализ интертипных отношений с позиции группы биполярных признаков.
Выберем в качестве характеристики бинарного отношения между парой типов ИМ спектр совпадающих в данном отношении признаков.
Таблица 3. Формы малых групп


* Однородные группы.
Таблица 4. Таблица умножения отношений в целостной группе

где P1, P2 иP3, — отношения в группе, T — тождественное отношение.
Таблица 5. Спектральная характеристика интертипных отношений в соционе

Анализ таблицы 1 с этих позиций показывает, что между шестнадцатью типами в соционе существует всего шестнадцать типов бинарных отношений, включая тождественные. Результаты этого анализа приведены в таблице 5.
Таблица 6. Асимметричные отношения

Таблица 7. Спектры отношений. (м, ро, д, пД)

где m, x, t и w — обозначения спектров.
Из таблицы 5 легко видеть:
1. Отношения в своей квадре и отношения с членами противоположной квадры однозначно соответствуют определённым спектрам.
2. Отношениям заказа и контроля соответствуют по два разных спектра.
3. Спектрам, обозначенным греческими буквами m, x, t и w, соответствуют по два вида отношений.
4. Отношениям м, ро, д, пД в зависимости от признака X10 входящих в него типов соответствуют разные спектры признаков.
Таким образом, в имеющейся в настоящее время таблице интертипных отношений нет полного соответствия между обозначениями отношения и их спектральными характеристиками.
Рассмотрим подробнее создавшуюся ситуацию.
1. Расщепление асимметричных отношений
Как видно из таблицы 5, в асимметричных отношениях легко выделить два типа отношений:
1. Рациональные.
Рациональный тип ? иррациональный тип.
2. Иррациональные.
Иррациональный тип ? рациональный тип.
Таблица 8. Таблица интертипных отношений

Отношения:

В рациональных отношениях (табл. 6) заказчиком или контролёром является рациональный тип, а в иррациональных - наоборот. Отличается ли содержательно один тип отношений заказа и контроля от другого и если отличается, то чем, - нам пока неизвестно. Однако введение такого разделения вместо прежнего - заказчик > приёмник, контролёр > подконтрольный, во первых, приводит в соответствие спектры отношений и их обозначения, а во вторых, позволяет, не нарушая смысла асимметричных отношений, рассматривать их математически единообразно с симметричными. Такое единообразие существенно облегчает анализ отношений в малых группах.
2. Расщепление отношений в м, д, ро и пД
В этом случае ситуация более серьёзна, чем с асимметричными отношениями. С одной стороны, в "Теории интертипных отношений" описаны четыре симметричных отношения, у которых нет однозначного соответствия с каким либо спектром признаков (табл. 5), с другой стороны, имеется четыре спектра, у которых нет однозначного соответствия с каким либо отношением.
В таблице 7 приведены отдельно спектры рассматриваемых отношений.
Если принять, что спектры m, x, t и w являются характеристиками определённых бинарных отношений между типами, как это имеет место во всех остальных случаях, тогда потребуется дополнительный анализ этих типов отношений и внесение соответствующих изменений в теорию интертипных отношений. Если это не так, то мы имеем дело с отношениями особого сорта, которые для циклотимов имеют одну спектральную характеристику, а для шизотимов — другую.
В случае полного соответствия отношений своим спектральным характеристикам, таблица интертипных отношений будет иметь вид гораздо более симметричный, чем в первоначальном варианте (табл. 8).
Построение этого варианта таблицы интертипных отношений позволяет нам перейти к анализу психологических форм более сложных, чем пара — типологии малых групп.
Литература:
- Аугустинавичюте А. Теория интертипных отношений. //Соционика, ментология и психология личности. - 1997. - №№ 1 5.
- Рейнин Г. Р. Группа биполярных признаков в типологии К. Г. Юнга. //Соционика, ментология и психология личности. - 1996. - № 6.
- Аугустинавичюте А. О дуальной природе человека. //Соционика, ментология и психология личности. - 1996. - №№ 1 3.
- Аугустинавичюте А. Социон. //Соционика, ментология и психология личности. - 1996. -№№ 4-5.
--------------------------------------------------------------------------------
- Работа написана в 1986 году. Её фрагмент опубликован в № 3 журнала "Соционика, ментология и психология личности" за 1996 год под названием "Типология малых групп". вернуться
- Социон - множество, состоящее из шестнадцати типов информационного метаболизма [3, 4]. вернуться
- В таблице приведены рабочие названия признаков и принят квадровый порядок расположения типов.
2002 г. © Г.Р. Рейнин






 станете более успешным в работе!
станете более успешным в работе!
